info@gerb.com
Caso di studio sulle tecnologie di smorzamento per edifici alti: Comfort e sicurezza
Linee guida per i sistemi di smorzamento del Council on Tall Buildings and Urban Habitat (CTBUH)
Thyssen Krupp Test Tower, Rottweil/Germania
Dati del progetto
- Anno di completamento:
2016 (completamento in altezza) - Sviluppatore/committente/proprietario:
Krupp Hoesch Stahl GmbH/Thyssen Krupp Elevators - Progettista architettonico:
Werner Sobek con JAHN Architects, Stoccarda e Chicago - Progettista strutturale:
Werner Sobek, Stoccarda - Fornitore del sistema di smorzamento:
GERB Vibration Control Systems - Laboratorio di prova:
Wacker Ingenieure (progettazione aerodinamica/prove nella galleria del vento) - Altezza/altezza interpiano:
246 m/3,3 m (zona uffici) - Rapporto di snellezza:
1/11,8 - Piani:
27 livelli/zona uffici di 8 piani - Superficie totale della torre:
340 metri quadrati - Funzione dell’edificio:
Torre di prova per ascensori/uffici/piattaforma di osservazione (232 m) - Materiale strutturale:
Cemento armato (C50/60)/facciata con membrana in PTFE su una struttura in acciaio - Sistema strutturale:
Nucleo a sbalzo in cemento armato su una fondazione a zattera
(-32 m) - Strategia di smorzamento utilizzata:
Sistema di smorzamento a massa ibrido (240 t)

1.0 Introduzione/storia
Nella Germania sud-occidentale è stata costruita una torre di 246 m di altezza per ospitare una struttura di prova per soluzioni innovative per gli ascensori. La torre ha un’impronta al suolo circolare con un diametro di 20 m e offre uno spazio di 9 vani per la prova degli ascensori, un ascensore antincendio e un ascensore a vista panoramica in vetro. È inoltre presente uno scambio di 220 m da utilizzare come vano per il sollevamento meccanico, destinato alla realizzazione dei programmi di prova.
La base della torre ha un diametro di 40 m per fornire ulteriore spazio alle strutture di servizio, alla zona di ingresso e a un centro di formazione. Al livello di 232 m, una piattaforma di osservazione – la più alta della Germania – consente una visione spettacolare della Foresta Nera e, durante le giornate limpide, persino delle Alpi.

2.0 Sistema strutturale
Il sistema strutturale della Test Tower è costituito, fondamentalmente, da un cilindro di cemento armato con un diametro di 20,8 m, ancorato per 30 m all’interno del terreno circostante (si veda la Figura 2). Fino a 110 m di altezza, il cilindro ha uno spessore di 40 cm, dopodiché di 25 cm. Il terreno, costituito da uno strato di Keuper e da calcare fossilifero sottostante, fornisce un’elevata capacità portante, perciò non si è resa necessaria una fondazione su pali. Oltre all’ancoraggio nel terreno circostante, la struttura allargata della base della torre fornisce ulteriore rigidezza laterale.
L’irrigidimento interno del cilindro in cemento armato è realizzato principalmente grazie alle pareti interne dei vani ascensore. Solo a determinati livelli di altezza sono state installate lastre prefabbricate per soffitti per consentire l’accesso ai vani ascensore. Alcuni vani ascensore terminano a un’altezza di 115 m e sono coperti da pavimentazioni a campata lunga con uno spessore di 40 cm, gettate in opera. Questi pavimenti vengono utilizzati per la zona uffici. Al di sopra, uno spazio vuoto fino a un livello di 197 m viene utilizzato come riserva di calore e per il sistema TMD. La parte alta della torre viene utilizzata come zona uffici e per i restanti vani ascensore.

Una caratteristica distintiva della Test Tower è la facciata tessile, realizzata con una maglia in fibra di vetro rivestita con PTFE. La larghezza dell’apertura della maglia aumenta con l’altezza dell’edificio per andare a incrementare la semitrasparenza della facciata, diminuire la densità e il peso del materiale e per gli effetti aerodinamici.
La forma a spirale della facciata è progettata per funzionare come un’elica Scruton e il tessuto stesso contribuisce a ombreggiare la struttura in cemento per evitare le sollecitazioni termiche dovute alla radiazione solare. Nell’ambito della progettazione della facciata e della scelta dei materiali è stato necessario considerare gli aspetti relativi all’installazione, alla manutenzione e alla durata, oltre al carico aerodinamico.
3.0 Metodo di costruzione

La costruzione della Test Tower è stata effettuata nelle seguenti fasi:
- Scavo di una fossa di costruzione circolare di 30 m per la base della torre. Lo scavo e la forma sono stati ottenuti tramite un’esplosione iniziale. Dopo lo scavo, la fossa è stata messa in sicurezza con tiranti nel terreno e rivestimento in calcestruzzo.
- Getto della fondazione a zattera
- Costruzione della struttura verticale in cemento utilizzando casseforme rampanti. Tutte le pareti sono state costruite in maniera continua in un periodo di 4 mesi.
- Costruzione delle solette per i pavimenti.
- Costruzione della zona di ingresso.
4.0 Risposta dinamica prevista al carico aerodinamico
Le frequenze fondamentali per la Test Tower sono state previste nell’intervallo 0,17 – 0,20 Hz, in base alla fase di costruzione e allo stato del cemento (con o senza crepe) – si veda la Figura 4.
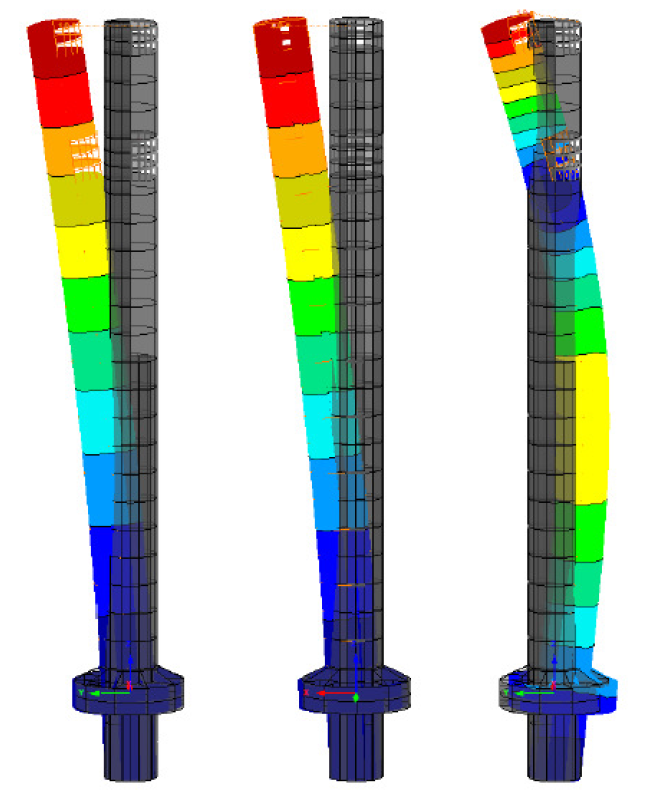
L’analisi aerodinamica ha rivelato che la sollecitazione risonante con la struttura può verificarsi in presenza di velocità del vento corrispondenti a valori al suolo (altezza 10 m) compresi nell’intervallo 55 – 60 km/h. Era previsto che, in assenza di ulteriore smorzamento, questa sollecitazione risonante potesse causare spostamenti sulla sommità di circa +/- 750 mm che, oltre a pregiudicare il comfort degli occupanti, avrebbero anche avuto conseguenze significative sulla ressistenza a fatica in esercizio della struttura in cemento della torre (si veda la Figura 5). Per ridurre la risposta dinamica alla sollecitazione da vento trasversale, è stato realizzato un sistema di smorzamento passivo a massa accordata. Poiché la torre sarebbe stata utilizzata come ambiente di prova per attrezzature relative agli ascensori, sensibili alle oscillazioni, il committente era alla ricerca di una possibilità di
sollecitazione artificiale della torre durante le giornate di calma, tuttavia con scostamenti che non provocassero problemi di fatica. Il livello richiesto per il movimento oscillatorio artificiale rientrava nell’intervallo, considerato sicuro, di circa +/- 200 mm. Questa richiesta ha fornito la rara opportunità di realizzare uno smorzatore a massa ibrido (HMD) oppure, visto che il sistema di progettazione differisce da quello degli altri sistemi HMD introdotti in passato, un cosiddetto TMD a duplice uso. Il sistema verrà presentato nei capitoli seguenti, assieme all’ottimizzazione del sistema passivo, alla progettazione del meccanismo degli attuatori, agli algoritmi di controllo e al progetto di sicurezza.

5.0 Ottimizzazione del sistema di smorzamento a massa accordata passivo
Per la determinazione dei parametri del sistema TMD passivo è stato necessario considerare tre diversi aspetti: a) fornire uno smorzamento strutturale aggiuntivo sufficiente a ridurre la risposta dinamica dovuta alla sollecitazione per distacco di vortice, b) limitare la conseguente oscillazione della massa principale del TMD in modalità passiva a un valore realizzabile/pratico nei momenti di sollecitazione da raffiche di vento trasversale e c) scegliere la massa del TMD in base alla quantità di energia necessaria per ottenere lo spostamento massimo della torre in corrispondenza del modo sollecitato, considerando i limiti prestazionali consentiti dagli attuatori forniti
(ossia la massima forza generata e la corsa massima durante il funzionamento). Per ottimizzare il sistema TMD, è stato utilizzato un modello numerico in cui erano rappresentati la distribuzione della massa della torre e i momenti di inerzia della massa documentati nelle proprietà strutturali identificate. Anche gli elementi di irrigidimento tra i piani sono stati adattati in modo da corrispondere alle forme modali e alle frequenze naturali durante le osservazioni a piena scala. La Figura 6 a sinistra mostra le forme modali e le frequenze naturali di questo modello analogico utilizzato. La Figura 6 a sinistra confronta anche le forme modali del modello analogico con quelle del modello dettagliato preparato dal consulente strutturale.
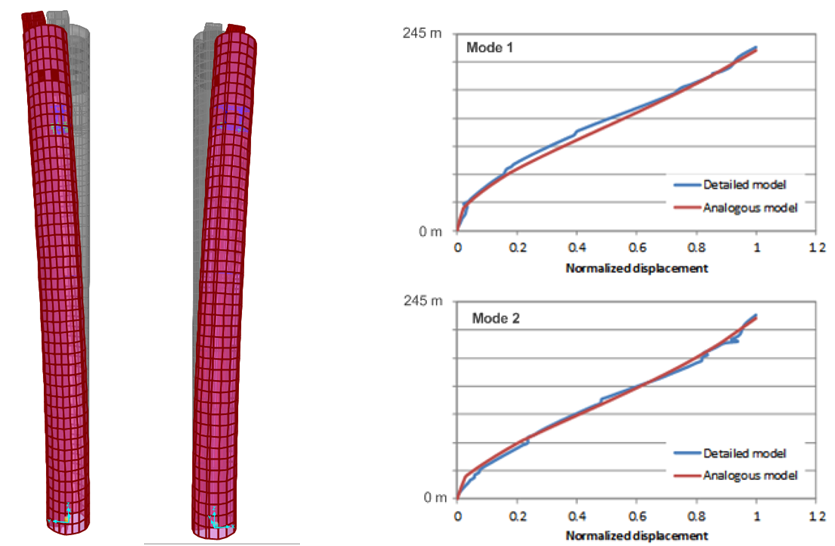
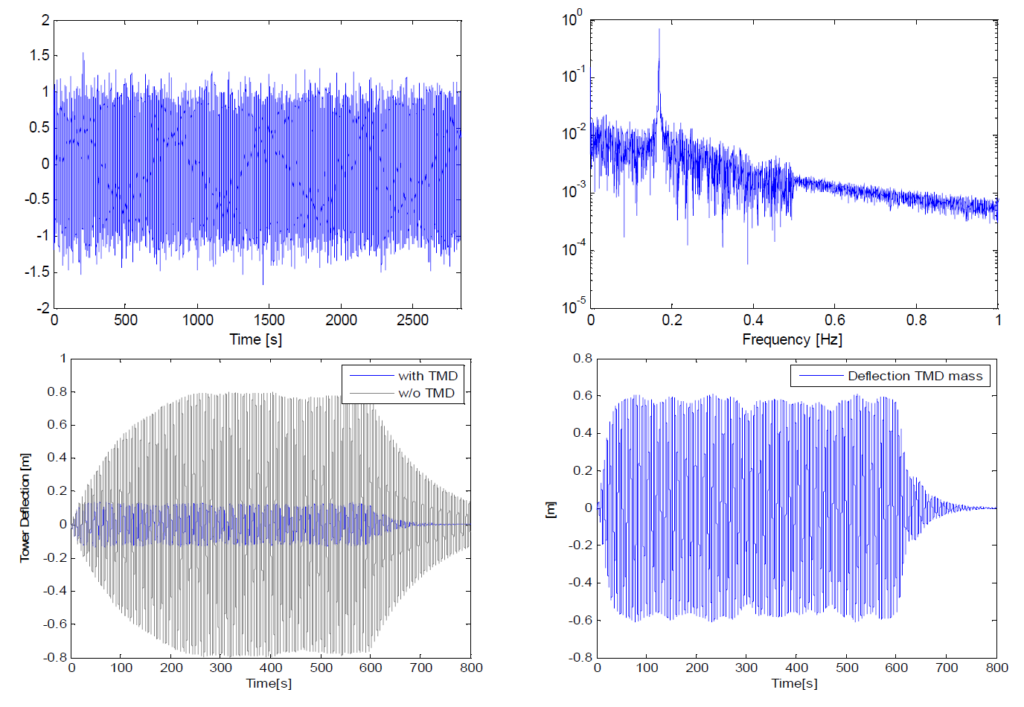
Inoltre, il TMD è stato modellato in modo discreto, come un sistema a pendolo, tenendo conto anche della sua posizione eccentrica sulla torre. Le caratteristiche di carico nel caso di input in esame, ossia la sollecitazione risonante dovuta al distacco di vortice, sono molto simili a quelle di una singola eccitazione armonica. Tuttavia, il carico contemporaneo dovuto alle raffiche di vento è, intrinsecamente, di natura stocastica e ad esso si applicano criteri di ottimizzazione diversi dal conosciuto criterio di Den Hartog. In più, gli spostamenti relativi della massa del TMD sono maggiori quando il carico è di tipo stocastico piuttosto che armonico. Poiché, per la determinazione numerica dei parametri ottimali per il TMD, è necessario considerare un carico simile a quello reale, è stato generato uno storico temporale comprendente sia il carico stocastico dovuto alle raffiche (basato sullo spettro di Davenport) e un componente con una risonanza sovrapposta, simile a quella della dissipazione dei vortici, per rappresentare la sollecitazione totale da vento trasversale (si veda la Figura 3 a destra). La riduzione della deflessione della torre che può essere ottenuta con il sistema TMD passivo ottimizzato, nonché gli spostamenti del TMD risultanti, sono illustrati nella Figura 3 a destra.
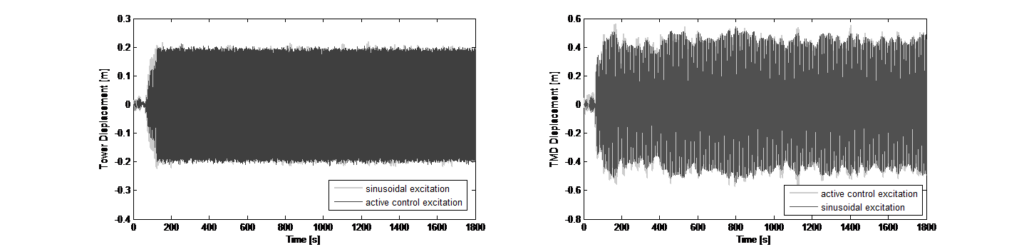
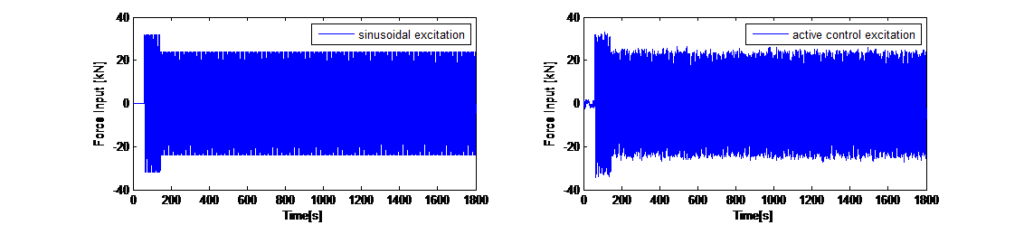
In base a questi risultati relativi a uno smorzamento strutturale intrinseco stimato in ξ=0,8%, è stato calcolato che era necessaria una massa del TMD di 240 t per mantenere le oscillazioni entro +/- 650 mm, preservando al contempo un coefficiente di smorzamento ottimale per il TMD, in modo da ottimizzare le prestazioni di quest’ultimo. Un aumento dello smorzamento del TMD avrebbe ridotto la corsa, mentre l’efficacia sarebbe rimasta comunque sufficiente; ciò tuttavia avrebbe avuto implicazioni negative sui requisiti relativi alle forze sugli attuatori. Per la determinazione delle forze necessarie per la configurazione ottimale del TMD da 240 t è stato utilizzato anche il modello analogico per verificare che, con una forza massima di 40 kN dagli attuatori, fosse possibile ottenere deflessioni della torre entro l’intervallo di +/- 200 mm. La Figura 4 illustra i risultati di una simulazione numerica nel dominio del tempo in base al modello numerico analogico; in questo caso vengono visualizzate le oscillazioni massime risultanti della sommità della torre, le oscillazioni della massa del TMD e le forze in ingresso attive che le provocano.


6.0 Descrizione del sistema di controllo
La dualità del sistema di controllo serve allo scopo a) di ridurre i consumi di energia, durante il normale funzionamento passivo, riducendo le vibrazioni che si verificano e b) di ridurre i requisiti relativi alle forze sugli attuatori, utilizzando effetti di risonanza per eccitare la massa principale del TMD soddisfacendo così, alla fine, la domanda di forza effettiva. Pertanto, rispetto ad altri sistemi di controllo (si veda la Figura 1), gli attuatori collegano la struttura principale alla massa del TMD, ma non vengono utilizzati per controllare direttamente tale massa, come normalmente accade in un tipico sistema con azionamento massa/smorzatore attivo.
Per il duplice uso implementato, è stata scelta una massa di reazione per l’azionamento passivo di 240 tonnellate. Per la modalità di eccitazione, due attuatori lineari – uno in ciascuna direzione principale – vengono collegati alla massa del TMD vicino al centro di gravità della massa, per evitare qualsiasi artefatto torsionale. Ogni attuatore lineare può fornire forze fino a 40 kN entro una corsa di max +/- 600 mm (si veda il dettaglio nella Figura 2). Gli azionamenti lineari possono essere staccati, in modo tale che la modalità completamente passiva non venga influenzata dai cuscinetti degli attuatori, nel raro caso di un loro guasto.
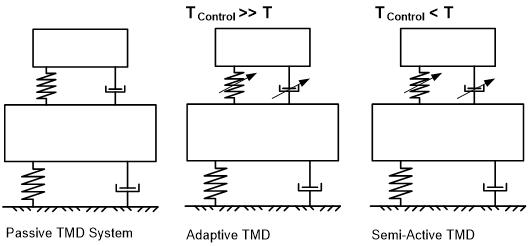
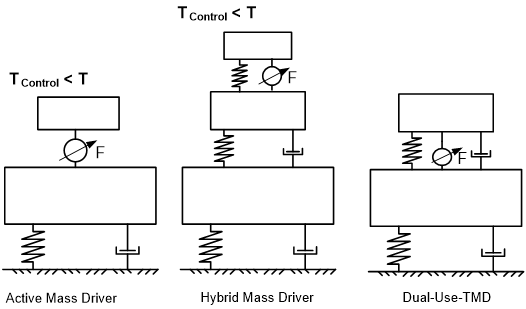
Figura 10 – Tipi di sistemi di controllo – TMD a duplice uso rispetto ai sistemi passivi, semi-attivi, attivi e ibridi
Il sistema è dotato di quattro accelerometri monoassiali (K-beam sismico/MEMS; uno in ogni direzione) per determinare il livello della sommità della torre e le accelerazioni della massa del TMD. I segnali di accelerazione vengono filtrati in un filtro passa-banda entro l’intervallo di frequenze naturali fondamentali della torre (0,1 – 0,3 Hz) e integrati per ottenere le velocità e le deflessioni della torre.
In più, i valori di spostamento integrati possono essere confrontati con quelli di un sistema di navigazione satellitare globale aggiuntivo, installato anch’esso sulla sommità per individuare derive dei segnali. A questo proposito è stato effettuato un test di correlazione iniziale. Inoltre, gli spostamenti del TMD vengono monitorati direttamente con estensimetri e un sistema induttivo di misurazione della lunghezza integrato nei motori lineari.
7.0 Algoritmo di controllo
Il ciclo di controllo generale della torre è illustrato alla Figura 5, che descrive la sequenza di controllo a ciclo chiuso. Una progettazione dettagliata dell’algoritmo di controllo richiederebbe modelli analitici dell’interazione tra attuatori e massa del TMD per determinare la connessione tra l’input dell’attuatore e la forza applicata all’azione. Questi modelli dovrebbero essere combinati con il modello analitico della struttura principale, che descrive il comportamento dinamico generale dell’edificio. Inoltre, rispetto agli algoritmi di controllo standard utilizzati per altre applicazioni HMD come in [2],[3] o ricercati in via teorica come in [1] l’algoritmo di controllo da applicare a questa torre doveva tenere conto di un’eccitazione sincrona controllata in una direzione principale e la riduzione delle vibrazioni in direzione perpendicolare. Dato che la risposta dinamica è prevista prevalentemente nei modi fondamentali, è stato possibile utilizzare, per entrambe queste operazioni, il controllo lineare del feedback, con tutti i suoi vantaggi di prevenzione delle instabilità. Questo perché la semplice realizzazione implementata per il controllo, il controllo lineare del feedback, che attenua la risposta dinamica della torre in direzione perpendicolare all’eccitazione, agisce sull’attuatore corrispondente attraverso una specifica somma lineare pesata di sette misurazioni dinamiche strutturali. Queste misurazioni sono: le accelerazioni del TMD e della sommità della torre, le velocità del TMD e della sommità della torre, gli spostamenti del TMD e della sommità della torre e lo spostamento relativo del TMD rispetto alla sommità della torre.
È importante notare che i fattori di pesatura preselezionati sono guadagni scalari semplici, positivi o negativi. La parametrizzazione dei fattori di pesatura è basata sui test dinamici della torre e non utilizza alcuna modifica dipendente dalla frequenza. Il feedback dell’attuatore attivo viene calcolato istantaneamente (a 50 Hz) ed è, nuovamente, una combinazione lineare delle misurazioni dinamiche precedenti. Non viene utilizzata alcuna manipolazione non lineare. Il progetto del controllo è stato implementato anche in una simulazione numerica nel dominio del tempo (ossia un’integrazione diretta) per comprovare le prestazioni di riduzione delle vibrazioni da parte del controllo dell’attuatore. Per la modalità di eccitazione è stato utilizzato lo stesso approccio di controllo, in combinazione con un offset di spostamento che rappresenta l’eccitazione della torre fino al valore di spostamento desiderato. Questo offset è una funzione sinusoidale basata sulla frequenza fondamentale rilevata in ciascuna direzione. L’uscita del controllo per controbilanciare la variazione dello spostamento della sommità dovuto ad altri disturbi viene poi modulata sulla funzione sinusoidale di offset e il valore di controllo viene adattato di conseguenza.
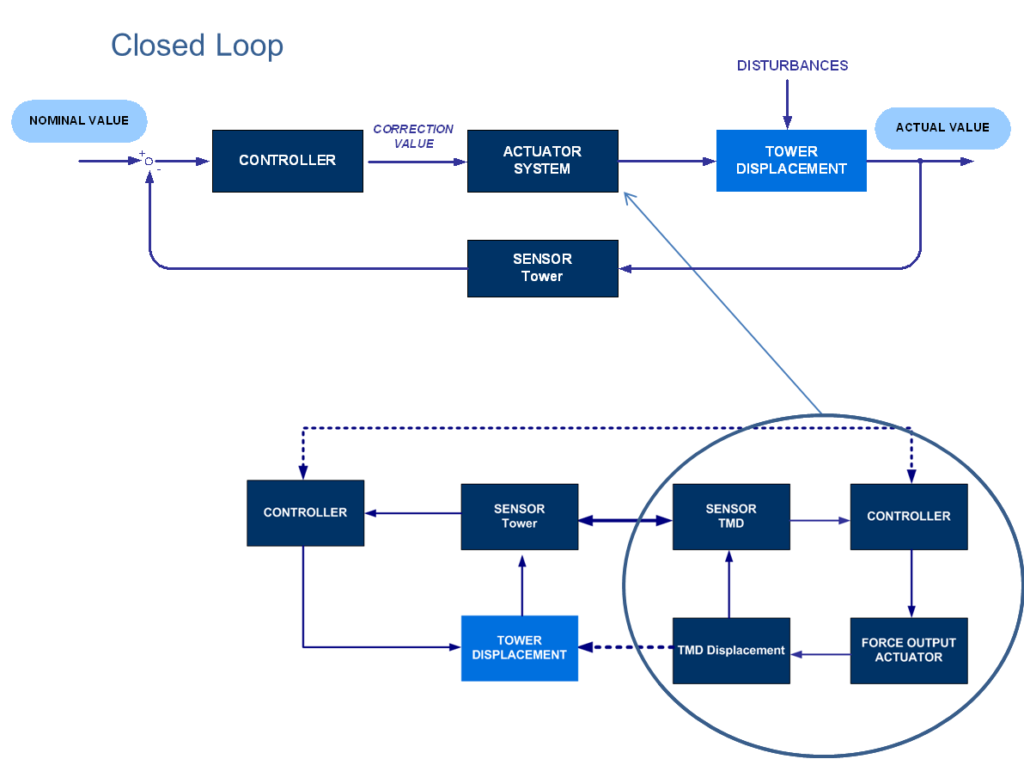
Il controllo lineare del feedback, che attenua la risposta dinamica della torre in direzione perpendicolare all’eccitazione, consente al comando di forza inviato all’attuatore di essere pari alla specifica somma lineare pesata delle sette misurazioni dinamiche del programma. Le sette misurazioni sono: le accelerazioni del TMD e della torre, le velocità del TMD e della torre, gli spostamenti del TMD e della torre e lo spostamento relativo del TMD rispetto alla torre. È importante notare che i fattori di pesatura sono valori scalari semplici, positivi o negativi. La parametrizzazione dei fattori di pesatura è basata sui test dinamici sperimentali della torre. Il feedback dell’attuatore attivo viene calcolato istantaneamente (50 Hz)
e i fattori di pesatura sono valori scalari che non utilizzano alcun tipo di funzione di trasferimento dipendente dalla frequenza. Inoltre, il feedback è una combinazione lineare della proprietà dinamica. Non viene utilizzata alcuna manipolazione o logica non lineare. Il progetto del controllo è stato implementato nell’ambito di una simulazione numerica nel dominio del tempo (integrazione diretta) per cui, per ogni intervallo di tempo, è stato possibile adattare l’input della forza verso la massa del TMD tramite il controllo dell’attuatore. La Figura 12 illustra i risultati della simulazione relativa alla soppressione delle vibrazioni – gli spostamenti della torre e il relativo spostamento della massa del TMD.
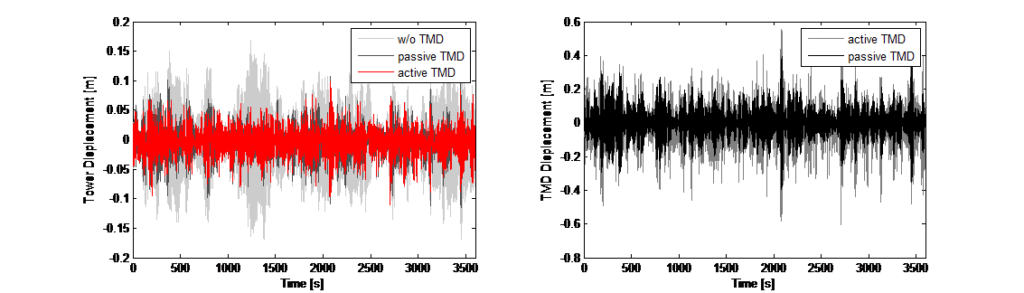
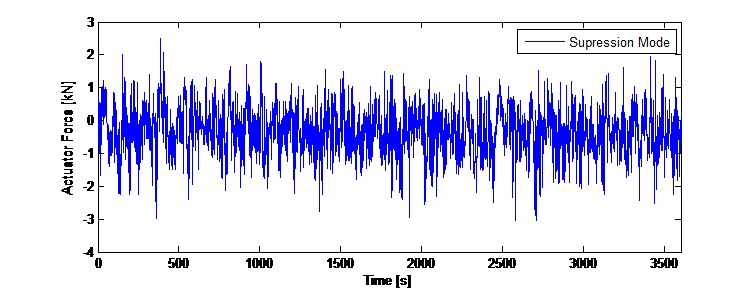
Per la modalità di eccitazione, è stato utilizzato lo stesso approccio di controllo, in combinazione con un offset che rappresenta l’eccitazione della torre fino al valore di spostamento desiderato. Questo offset è una funzione sinusoidale basata sulla frequenza fondamentale rilevata in ciascuna direzione. L’uscita del controllo per controbilanciare la variazione dello spostamento della sommità dovuto al disturbo viene poi modulata sulla funzione sinusoidale di offset
e il valore di controllo deve essere adattato in modo corrispondente. Per questo offset è stato stabilito in via sperimentale un fattore di pesatura. La Figura 13 mostra i risultati numerici con disturbo dovuto a carico da raffiche di vento per la modalità di eccitazione, con una semplice eccitazione sinusoidale e con l’algoritmo di controllo applicato.
8.0 Progetto di sicurezza
Considerando la forza di +/- 40 kN che può essere fornita dagli azionamenti lineari utilizzati come attuatori, è indispensabile un progetto di sicurezza per assicurare che gli spostamenti della torre non superino i llimiti di fatica. Questo vale anche se l’uscita di forza non è sufficiente a causare deflessioni della sommità maggiori dei +/- 200 mm prestabiliti. Un approccio per migliorare la sicurezza del sistema era quello di aumentare la ridondanza dei sensori di monitoraggio che registrano la deflessione della sommità della torre. Il modo migliore per farlo consiste nell’applicazione di un sistema di monitoraggio aggiuntivo indipendente che, nel caso ideale, utilizza un principio di misurazione diverso da quello dell’hardware di controllo vero e proprio. Per il progetto qui presentato, l’hardware di controllo prevedeva, come sopra indicato, accelerometri e una soglia definita di accelerazione per il filtraggio passa-banda del segnale nell’intervallo di frequenze naturali rilevanti per la struttura. Il sistema di monitoraggio sovraordinato prioritario è un Sistema satellitare globale di navigazione (GNSS) con un’accuratezza di +/- 10 mm.
Il sistema GNSS richiede una stazione di base di riferimento che elabora i dati relativi alle coordinate per ricavare i valori di risposta dello spostamento vero e proprio. Se la sommità della torre supera una soglia predeterminata durante il modo di eccitazione artificiale, un fatto che può essere dovuto al vento o ad altra eccitazione, un relè commuta il segnale di attesa su 0 V e ciò provoca l’interruzione del modo di eccitazione. In più, entrambi i sistemi di monitoraggio controllano costantemente i dati acquisiti, individuando segnali da sensori difettosi che provocano anch’essi l’interruzione del modo di eccitazione attivo. I segnali difettosi di accelerazione/di estensione del cavo vengono rilevati attraverso un criterio spettrale di rilevamento dei picchi – è possibile presumere che i sensori forniscano segnali legittimi solo se il rilevamento dei picchi è possibile in un intervallo pertinente. Mentre il sistema GNSS analizza la modifica dei dati relativi alle coordinate, se i dati campionati non cambiano in tempo si presume automaticamente che il segnale sia difettoso.
9.0 Prove delle vibrazioni
I test iniziali delle vibrazioni della torre sono stati effettuati allo stato attuale, con la torre non ancora completata, per cui le frequenze fondamentali della torre a questo stadio risultano al di sopra dell’intervallo di taratura specificato del sistema TMD passivo. Il TMD viene regolato sulla frequenza di taratura massima possibile. L’obiettivo delle prove delle vibrazioni consisteva da una parte nel determinare le frequenze fondamentali della torre con il sistema TMD bloccato e dall’altra determinare lo smorzamento strutturale. Era inoltre necessario determinare il comportamento dinamico con il TMD passivo in funzione, oltre all’aumento dello smorzamento strutturale dovuto al TMD stesso. Per identificare le frequenze naturali fondamentali della torre è possibile utilizzare il metodo della densità spettrale di potenza [1] normalizzata media (ANPSD). A questo scopo, i diagrammi nel dominio del tempo registrati devono essere divisi in segmenti, i quali devono essere trasformati nel dominio della frequenza. Gli spettri risultanti devono essere normalizzati e ne deve essere calcolata la media; quindi devono essere moltiplicati per gli spettri coniugati complessi.
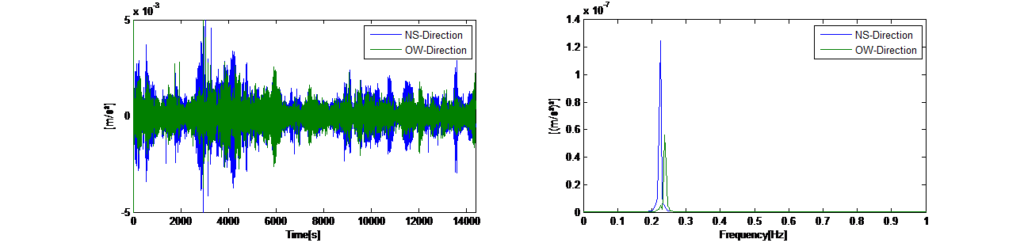
Così facendo vengono eliminate tutte le vibrazioni casuali e solo le vibrazioni libere ricorrenti della struttura verranno visualizzate nello spettro medio, che ora rappresenta le frequenze naturali della torre con l’eccitazione dominante. La Figura 14 a sinistra mostra gli storici temporali registrati delle vibrazioni ambientali orizzontali nelle direzioni x e y con il TMD bloccato. La Figura 14 a destra mostra gli spettri Auto Power medi di una finestra di 120 secondi. Gli spettri indicano che la torre evidenzia una risposta dinamica a due frequenze dominanti (0,225 Hz in direzione x e 0,245 Hz in direzione y).
Oltre al sopra citato metodo spettrale della potenza media – nel quale si presume che la sollecitazione ambientale provochi una risposta dinamica, nei modi di vibrare rilevanti, sufficiente ad ottenere una sicurezza stocastica – le frequenze naturali sono state determinate utilizzando il software di elaborazione dei segnali ARTEMIS, [1] che include i metodi di decomposizione amplificata del dominio della frequenza e di identificazione del sottospazio stocastico.
La decomposizione amplificata del dominio della frequenza (Enhanced Frequency Domain Decomposition, EFDD) e l’identificazione del sottospazio stocastico sono tecniche ampiamente utilizzate per l’identificazione dei parametri modali output-only.
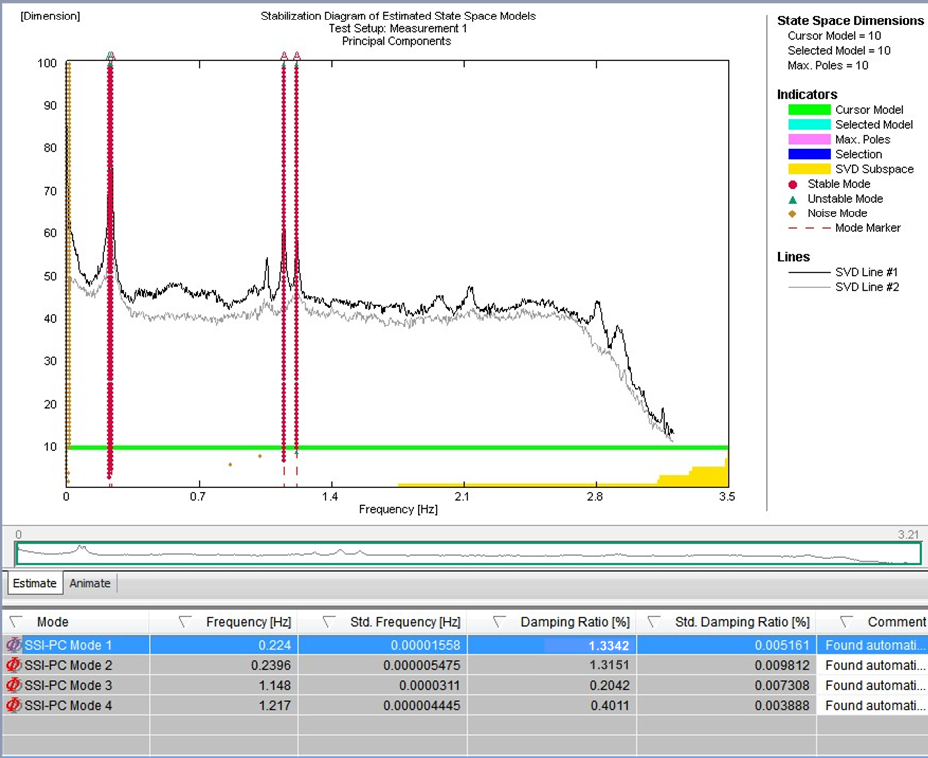
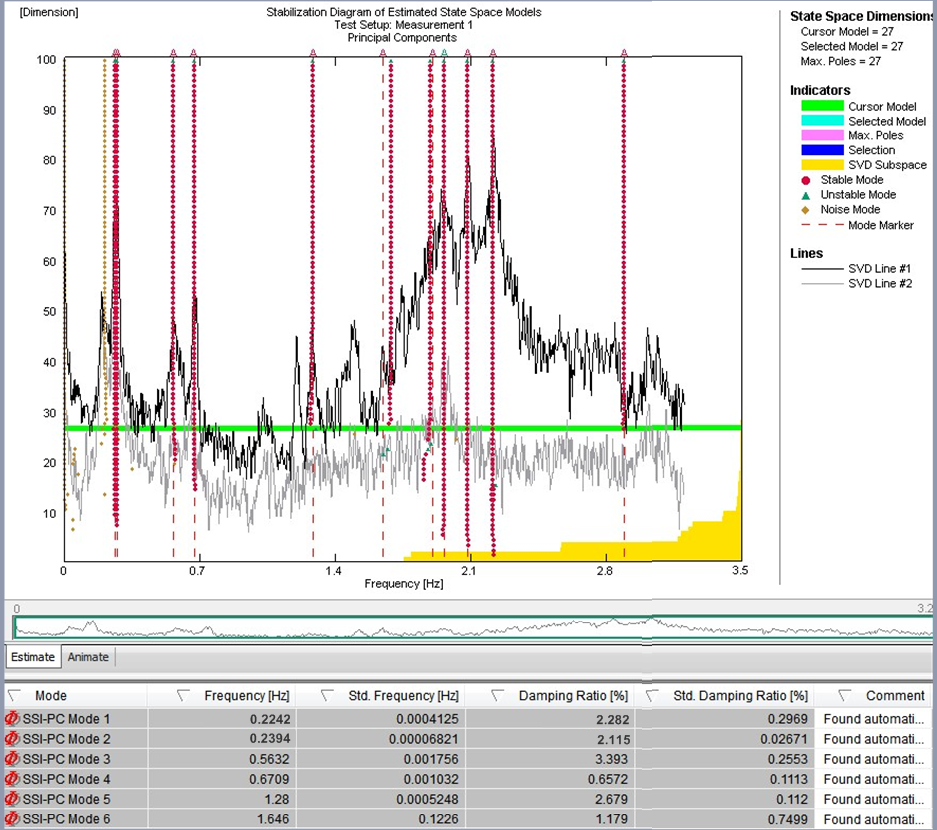
Figura 15 – Schemi della stabilità relativi alle registrazioni delle vibrazioni ambientali con TMD bloccato (a sinistra) e attivo (a destra)
Poiché il metodo EFDD si basa sul calcolo degli spettri di risposta, sono necessarie lunghe registrazioni per mantenere basso l’errore relativo alla stima dello spettro ed estrarre i parametri modali in modo affidabile. L’algoritmo di identificazione del sottospazio stocastico è stato utilizzato per identificare ponti utilizzando un modello output-only. I metodi di identificazione del sottospazio stocastico funzionano nel dominio del tempo e si basano una descrizione spaziale dello stato del problema dinamico. I risultati dell’identificazione del sistema con diversi ordini del modello vengono confrontati per distinguere tre modi strutturali dai modi spuri nei cosiddetti diagrammi di stabilizzazione, i quali rappresentano un’opzione diffusa per selezionare il modello del sistema identificato, in quanto i veri modi strutturali tendono a essere stabili nei successivi ordini dei modelli, soddisfacendo certi criteri di stabilizzazione che vengono valutati in una procedura automatizzata. La Figura 15 illustra uno schema di stabilità risultante dai dati dell’ambiente registrati, dai quali possono essere determinati i modi rilevanti. I modi identificati e i rapporti di smorzamento individuati per ciascun modo nello stato con TMD bloccato (a sinistra) e TMD in funzione (a destra) vengono illustrati anch’essi nella Figura 14. È possibile notare un aumento dello smorzamento strutturale. Lo smorzamento strutturale aggiuntivo rientra nell’intervallo di un valore teorico che può essere determinato a partire dal modello teorico per il quale è stata considerata la configurazione del TMD non tarato.
Oltre alle prove delle vibrazioni ambientali con il sistema TMD passivo, sono state effettuate prove preliminari con il sistema di eccitazione attiva, nonostante il TMD non fosse stato ancora tarato. La Figura 12 a sinistra illustra il diagramma delle accelerazioni nel dominio del tempo registrate sulla sommità della torre. Dopo un’eccitazione sinusoidale iniziale, l’algoritmo del livello di accelerazione costante è stato attivato per determinare in via sperimentale la correlazione tra la deflessione della torre e lo spostamento forzato della massa del TMD. il diagramma nel dominio del tempo illustrato nella Figura 12 visualizza i due scenari di test nel modo di eccitazione e gli spettri FFT corrispondenti mostrano l’evidente risposta della torre nelle sue due frequenze fondamentali (nelle direzioni x e y). La sezione temporale evidenziata in verde è un’eccitazione sinusoidale della massa con controllo attivo disabilitato, che ha causato una risposta dinamica in entrambe le direzioni principali. Lo spettro FFT risultante visualizza i due picchi per identificare le frequenze fondamentali in queste due direzioni. La finestra temporale evidenziata in blu riguarda un’eccitazione con controllo attivo in funzione che ha causato uno spostamento della torre più costante, prevalentemente in una direzione. Il risultante decadimento delle vibrazioni dopo la disattivazione del modo di eccitazione è stato utilizzato anche per determinare lo smorzamento strutturale ed è risultato pari a D=2,4%. Questo risultato coincide con il rapporto di smorzamento determinato con gli algoritmi SSI.
10.0 Conclusione e previsioni
Sulla Thyssen Krupp Test Tower, di 246 m di altezza, è stato installato un TMD a doppio effetto con l’obiettivo di eccitare intenzionalmente la torre fino a una riposta dinamica controllata nelle sue frequenze fondamentali. L’obiettivo di questa eccitazione è ottenere un’oscillazione controllata nelle due direzioni principali della torre. Sulla base di calcoli numerici, è stato ricavato che era necessaria una massa del TMD di 240 t per ottenere lo smorzamento supplementare richiesto per la modalità passiva e per generare la forza di controllo necessaria a ottenere uno spostamento della sommità della torre di +/- 200 mm. Per creare un livello di spostamento costante nella modalità di eccitazione e sopprimere gli spostamenti provocati dal vento, nonché la componente di vibrazione forzata nella direzione perpendicolare, è stato sviluppato un algoritmo di controllo, testato con simulazioni numeriche. Dopo l’installazione del TMD a pendolo passivo, per il quale sono state utilizzate delle lastre prefabbricate di cemento come massa di reazione, sono stati messi in servizio gli attuatori e sono stati effettuati i test iniziali, i quali hanno rivelato che lo smorzamento intrinseco della torre era maggiore di quanto previsto, ma è stato possibile determinare chiaramente tutti i modi significativi. Il modo di eccitazione attivo dell’edificio funziona ed è stato possibile testarlo, anche se non completamente, per derivare tutti parametri operativi, dal momento che l’edificio non è ancora del tutto ultimato. Dato che l’edificio non era stato ancora completato, non è stato possibile adeguare il TMD passivo alle frequenze fondamentali stabilite.
Una volta adattato il sistema TMD, saranno effettuate ulteriori prove nell’edificio, che comprenderanno anche test riguardanti lo smorzamento in dipendenza dall’ampiezza di oscillazione e l’intero progetto di sicurezza.
RIFERIMENTI
[1] Wenzel, H., Pichler, D., Schedler, R. (1991). „Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken“, Bauingenieur 74
[2] Döhler, M., Andersen, P.: Mevel, L. (2012). “Operational Modal Analysis using a Fast Stochastic Subspace Identification Method”, Conference Proceedings of the Society for Experimental Mechanics Series
[3] Soong, T.T., Spencer, J.R. (2000). “Active, Semi-Active and hybrid control of structures” In 12th World Conference for Earthquake Engineering
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003). Passive and active mass damper control of the response of tall buildings to wind gustiness. Eng. Struct., 25, 1199–1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings. J. Eng. Mech. 2004, 130, 437–446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building. Earthq. Eng. Struct. Dyn. 2001, 30, 1655–1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower. CTBUH J. 2012, 24–29.
[8] Soong, T.T. “Active Structural Control: Theory and Practice”; John Wiley & Sons, Inc.: New York, NY, USA, 1990
[9] Preumont, A., Kazuto, S. (2008).”Active Control of Structures”, Wiley, Padstow
Ulteriori risorse
Vi servono ulteriori informazioni su questo argomento?
Non esitate a contattarci con domande specifiche.
Uno dei nostri ingegneri risponderà entro breve tempo alla richiesta.
Caso di studio sulle tecnologie di smorzamento per edifici alti: Comfort e sicurezza
Linee guida per i sistemi di smorzamento del Council on Tall Buildings and Urban Habitat (CTBUH)
Thyssen Krupp Test Tower, Rottweil/Germania
Dati del progetto
- Anno di completamento:
2016 (completamento in altezza) - Sviluppatore/committente/proprietario:
Krupp Hoesch Stahl GmbH/Thyssen Krupp Elevators - Progettista architettonico:
Werner Sobek con JAHN Architects, Stoccarda e Chicago - Progettista strutturale:
Werner Sobek, Stoccarda - Fornitore del sistema di smorzamento:
GERB Vibration Control Systems - Laboratorio di prova:
Wacker Ingenieure (progettazione aerodinamica/prove nella galleria del vento) - Altezza/altezza interpiano:
246 m/3,3 m (zona uffici) - Piani:
27 livelli/zona uffici di 8 piani - Superficie totale della torre:
340 metri quadrati - Funzione dell’edificio:
Torre di prova per ascensori/uffici/piattaforma di osservazione (232 m) - Strategia di smorzamento utilizzata:
Sistema di smorzamento a massa ibrido (240 t)

- Materiale strutturale:
Cemento armato (C50/60)/facciata con membrana in PTFE su una struttura in acciaio - Sistema strutturale:
Nucleo a sbalzo in cemento armato su una fondazione a zattera
(-32 m)
Caso di studio sulle tecnologie di smorzamento per edifici alti: Comfort e sicurezza
Linee guida per i sistemi di smorzamento del Council on Tall Buildings and Urban Habitat (CTBUH)
Thyssen Krupp Test Tower, Rottweil/Germania
Dati del progetto
- Anno di completamento: 2016 (completamento in altezza)
- Sviluppatore/committente/proprietario: Krupp Hoesch Stahl GmbH/Thyssen Krupp Elevators
- Progettista architettonico: Werner Sobek con JAHN Architects, Stoccarda e Chicago
- Progettista strutturale: Werner Sobek, Stoccarda
- Fornitore dello smorzamento: GERB Vibration Control Systems
- Laboratorio di prova: Wacker Ingenieure (progettazione aerodinamica/prove nella galleria del vento)
- Altezza/altezza interpiano: 246 m/3,3 m (zona uffici)
- Piani: 27 livelli/zona uffici di 8 piani
- Superficie lorda della torre: 340 metri quadrati
- Funzione dell’edificio: Torre di prova per ascensori/uffici/piattaforma di osservazione (232 m)
- Materiale strutturale: Cemento armato (C50/60)/facciata con membrana in PTFE su una struttura in acciaio
- Sistema strutturale: Nucleo a sbalzo in cemento armato su una fondazione a zattera (-32 m)
- Strategia di smorzamento utilizzata: Sistema di smorzamento a massa ibrido (240 t)

1.0 Introduzione/storia
Nella Germania sud-occidentale è stata costruita una torre di 246 m di altezza per ospitare una struttura di prova per soluzioni innovative per gli ascensori. La torre ha un’impronta al suolo circolare con un diametro di 20 m e offre uno spazio di 9 vani per la prova degli ascensori, un ascensore antincendio e un ascensore a vista panoramica in vetro. È inoltre presente uno scambio di 220 m da utilizzare come vano per il sollevamento meccanico, destinato alla realizzazione dei programmi di prova.
La base della torre ha un diametro di 40 m per fornire ulteriore spazio alle strutture di servizio, alla zona di ingresso e a un centro di formazione. Al livello di 232 m, una piattaforma di osservazione – la più alta della Germania – consente una visione spettacolare della Foresta Nera e, durante le giornate limpide, persino delle Alpi.

2.0 Sistema strutturale
Il sistema strutturale della Test Tower è costituito, fondamentalmente, da un cilindro di cemento armato con un diametro di 20,8 m, ancorato per 30 m all’interno del terreno circostante (si veda la Figura 2). Fino a 110 m di altezza, il cilindro ha uno spessore di 40 cm, dopodiché di 25 cm. Il terreno, costituito da uno strato di Keuper e da calcare fossilifero sottostante, fornisce un’elevata capacità portante, perciò non si è resa necessaria una fondazione su pali. Oltre all’ancoraggio nel terreno circostante, la struttura allargata della base della torre fornisce ulteriore rigidezza laterale.
L’irrigidimento interno del cilindro in cemento armato è realizzato principalmente grazie alle pareti interne dei vani ascensore. Solo a determinati livelli di altezza sono state installate lastre prefabbricate per soffitti per consentire l’accesso ai vani ascensore. Alcuni vani ascensore terminano a un’altezza di 115 m e sono coperti da pavimentazioni a campata lunga con uno spessore di 40 cm, gettate in opera. Questi pavimenti vengono utilizzati per la zona uffici. Al di sopra, uno spazio vuoto fino a un livello di 197 m viene utilizzato come riserva di calore e per il sistema TMD. La parte alta della torre viene utilizzata come zona uffici e per i restanti vani ascensore.

Una caratteristica distintiva della Test Tower è la facciata tessile, realizzata con una maglia in fibra di vetro rivestita con PTFE. La larghezza dell’apertura della maglia aumenta con l’altezza dell’edificio per andare a incrementare la semitrasparenza della facciata, diminuire la densità e il peso del materiale e per gli effetti aerodinamici.
La forma a spirale della facciata è progettata per funzionare come un’elica Scruton e il tessuto stesso contribuisce a ombreggiare la struttura in cemento per evitare le sollecitazioni termiche dovute alla radiazione solare. Nell’ambito della progettazione della facciata e della scelta dei materiali è stato necessario considerare gli aspetti relativi all’installazione, alla manutenzione e alla durata, oltre al carico aerodinamico.
3.0 Metodo di costruzione

La costruzione della Test Tower è stata effettuata nelle seguenti fasi:
- Scavo di una fossa di costruzione circolare di 30 m per la base della torre. Lo scavo e la forma sono stati ottenuti tramite un’esplosione iniziale. Dopo lo scavo, la fossa è stata messa in sicurezza con tiranti nel terreno e rivestimento in calcestruzzo.
- Getto della fondazione a zattera
- Costruzione della struttura verticale in cemento utilizzando casseforme rampanti. Tutte le pareti sono state costruite in maniera continua in un periodo di 4 mesi.
- Costruzione delle solette per i pavimenti.
- Costruzione della zona di ingresso.
4.0 Risposta dinamica prevista al carico aerodinamico
Le frequenze fondamentali per la Test Tower sono state previste nell’intervallo 0,17 – 0,20 Hz, in base alla fase di costruzione e allo stato del cemento (con o senza crepe) – si veda la Figura 4.

L’analisi aerodinamica ha rivelato che la sollecitazione risonante con la struttura può verificarsi in presenza di velocità del vento corrispondenti a valori al suolo (altezza 10 m) compresi nell’intervallo 55 – 60 km/h. Era previsto che, in assenza di ulteriore smorzamento, questa sollecitazione risonante potesse causare spostamenti sulla sommità di circa +/- 750 mm che, oltre a pregiudicare il comfort degli occupanti, avrebbero anche avuto conseguenze significative sulla ressistenza a fatica in esercizio della struttura in cemento della torre (si veda la Figura 5). Per ridurre la risposta dinamica alla sollecitazione da vento trasversale, è stato realizzato un sistema di smorzamento passivo a massa accordata. Poiché la torre sarebbe stata utilizzata come ambiente di prova per attrezzature relative agli ascensori, sensibili alle oscillazioni, il proprietario era alla ricerca di una possibilità di sollecitazione artificiale della torre durante le giornate di calma, tuttavia con scostamenti che non provocassero problemi di affaticamento. Il livello richiesto per il movimento oscillatorio artificiale rientrava nell’intervallo, considerato sicuro, di circa +/- 200 mm. Questa richiesta ha fornito la rara opportunità di realizzare uno smorzatore a massa ibrido (HMD) oppure, visto che il sistema di progettazione differisce da quello degli altri sistemi HMD introdotti in passato, un cosiddetto TMD a duplice uso. Il sistema verrà presentato nei capitoli seguenti, assieme all’ottimizzazione del sistema passivo, alla progettazione del meccanismo degli attuatori, agli algoritmi di controllo e al progetto di sicurezza.

5.0 Ottimizzazione del sistema di smorzamento a massa accordata passivo
Per la determinazione dei parametri del sistema TMD passivo è stato necessario considerare tre diversi aspetti: a) fornire uno smorzamento strutturale aggiuntivo sufficiente a ridurre la risposta dinamica dovuta alla sollecitazione per dissipazione dei vortici, b) limitare il conseguente scostamento della massa principale del TMD in modalità passiva a un valore realizzabile/pratico nei momenti di sollecitazione da raffiche di venti trasversali e c) scegliere la massa del TMD in base alla quantità di energia necessaria per ottenere la deflessione massima della torre nella modalità di sollecitazione, considerando i limiti prestazionali consentiti dagli attuatori forniti (ossia la massima forza generata e la corsa massima durante il funzionamento). Per ottimizzare il sistema TMD, è stato utilizzato un modello numerico in cui erano rappresentati la distribuzione della massa della torre e i momenti di inerzia della massa documentati nelle proprietà strutturali identificate. Anche gli elementi di irrigidimento tra i piani sono stati adattati in modo da corrispondere alle forme modali e alle frequenze naturali durante le osservazioni a piena scala. La Figura 6 a sinistra mostra le forme modali e le frequenze naturali di questo modello analogico utilizzato. La Figura 6 a sinistra confronta anche le curve modali del modello analogico con quelle del modello dettagliato preparato dal consulente strutturale.


Inoltre, il TMD è stato modellato in modo discreto, come un sistema a pendolo, tenendo conto anche della sua posizione eccentrica sulla torre. Le caratteristiche di carico nel caso di input in esame, ossia la sollecitazione risonante dovuta al distacco di vortice, sono molto simili a quelle di una singola eccitazione armonica. Tuttavia, il carico contemporaneo dovuto alle raffiche di vento è, intrinsecamente, di natura stocastica e ad esso si applicano criteri di ottimizzazione diversi dal conosciuto criterio di Den Hartog. In più, gli spostamenti relativi della massa del TMD sono maggiori quando il carico è di tipo stocastico piuttosto che armonico. Poiché, per la determinazione numerica dei parametri ottimali per il TMD, è necessario considerare un carico simile a quello reale, è stato generato uno storico temporale comprendente sia il carico stocastico dovuto alle raffiche (basato sullo spettro di Davenport) e un componente con una risonanza sovrapposta, simile a quella della dissipazione dei vortici, per rappresentare la sollecitazione totale da vento trasversale (si veda la Figura 3 a destra). La riduzione della deflessione della torre che può essere ottenuta con il sistema TMD passivo ottimizzato, nonché gli scostamenti del TMD risultanti, sono illustrati nella Figura 3 a destra.
In base a questi risultati relativi a uno smorzamento strutturale intrinseco stimato in ξ=0,8%, è stato calcolato che era necessaria una massa del TMD di 240 t per mantenere le oscillazioni entro +/- 650 mm, preservando al contempo un coefficiente di smorzamento ottimale per il TMD, in modo da ottimizzare le prestazioni di quest’ultimo. Un aumento dello smorzamento del TMD avrebbe ridotto la corsa, mentre l’efficacia sarebbe rimasta comunque sufficiente; ciò tuttavia avrebbe avuto implicazioni negative sui requisiti relativi alle forze sugli attuatori. Per la determinazione delle forze necessarie per la configurazione ottimale del TMD da 240 t è stato utilizzato anche il modello analogico per verificare che, con una forza massima di 40 kN dagli attuatori, fosse possibile ottenere deflessioni della torre entro l’intervallo di +/- 200 mm. La Figura 4 illustra i risultati di una simulazione numerica nel dominio del tempo in base al modello numerico analogico; in questo caso vengono visualizzate le oscillazioni massime risultanti della sommità della torre, le oscillazioni della massa del TMD e le forze in ingresso attive che le provocano.


6.0 Descrizione del sistema di controllo
La dualità del sistema di controllo serve allo scopo a) di ridurre i consumi di energia, durante il normale funzionamento passivo, riducendo le vibrazioni che si verificano e b) di ridurre i requisiti relativi alle forze sugli attuatori, utilizzando effetti di risonanza per eccitare la massa principale del TMD soddisfacendo così, alla fine, la domanda di forza effettiva. Pertanto, rispetto ad altri sistemi di controllo (si veda la Figura 1), gli attuatori collegano la struttura principale alla massa del TMD, ma non vengono utilizzati per controllare direttamente tale massa, come normalmente accade in un tipico sistema con azionamento massa/smorzatore attivo.
Per il duplice uso implementato, è stata scelta una massa di reazione per l’azionamento passivo di 240 tonnellate. Per la modalità di eccitazione, due attuatori lineari – uno in ciascuna direzione principale – vengono collegati alla massa del TMD vicino al centro di gravità della massa, per evitare qualsiasi artefatto torsionale. Ogni attuatore lineare può fornire forze fino a 40 kN entro una corsa di max +/- 600 mm (si veda il dettaglio nella Figura 2). Gli azionamenti lineari possono essere staccati, in modo tale che la modalità completamente passiva non venga influenzata dai cuscinetti degli attuatori, nel raro caso di un loro guasto.


Figura 10 – Tipi di sistemi di controllo – TMD a duplice uso rispetto ai sistemi passivi, semi-attivi, attivi e ibridi
Il sistema è dotato di quattro accelerometri monoassiali (K-beam sismico/MEMS; uno in ogni direzione) per determinare il livello della sommità della torre e le accelerazioni della massa del TMD. I segnali di accelerazione vengono filtrati in un filtro passa-banda entro l’intervallo di frequenze naturali fondamentali della torre (0,1 – 0,3 Hz) e integrati per ottenere le velocità e le deflessioni della torre.
In più, i valori di spostamento integrati possono essere confrontati con quelli di un sistema di navigazione satellitare globale aggiuntivo, installato anch’esso sulla sommità per individuare derive dei segnali. A questo proposito è stato effettuato un test di correlazione iniziale. Inoltre, gli spostamenti del TMD vengono monitorati direttamente con estensimetri e un sistema induttivo di misurazione della lunghezza integrato nei motori lineari.
7.0 Algoritmo di controllo
Il ciclo di controllo generale della torre è illustrato alla Figura 5, che descrive la sequenza di controllo a ciclo chiuso. Una progettazione dettagliata dell’algoritmo di controllo richiederebbe modelli analitici dell’interazione tra attuatori e massa del TMD per determinare la connessione tra l’input dell’attuatore e la forza applicata all’azione. Questi modelli dovrebbero essere combinati con il modello analitico della struttura principale, che descrive il comportamento dinamico generale dell’edificio. Inoltre, rispetto agli algoritmi di controllo standard utilizzati per altre applicazioni HMD come in [2],[3] o ricercati in via teorica come in [1] l’algoritmo di controllo da applicare a questa torre doveva tenere conto di un’eccitazione sincrona controllata in una direzione principale e la riduzione delle vibrazioni in direzione perpendicolare. Dato che la risposta dinamica è prevista prevalentemente nei modi fondamentali, è stato possibile utilizzare, per entrambe queste operazioni, il controllo lineare del feedback, con tutti i suoi vantaggi di prevenzione delle instabilità. Questo perché la semplice realizzazione implementata per il controllo, il controllo lineare del feedback, che attenua la risposta dinamica della torre in direzione perpendicolare all’eccitazione, agisce sull’attuatore corrispondente attraverso una specifica somma lineare pesata di sette misurazioni dinamiche strutturali. Queste misurazioni sono: le accelerazioni del TMD e della sommità della torre, le velocità del TMD e della sommità della torre, gli spostamenti del TMD e della sommità della torre e lo spostamento relativo del TMD rispetto alla sommità della torre.
È importante notare che i fattori di pesatura preselezionati sono guadagni scalari semplici, positivi o negativi. La parametrizzazione dei fattori di pesatura è basata sui test dinamici della torre e non utilizza alcuna modifica dipendente dalla frequenza. Il feedback dell’attuatore attivo viene calcolato istantaneamente (a 50 Hz) ed è, nuovamente, una combinazione lineare delle misurazioni dinamiche precedenti. Non viene utilizzata alcuna manipolazione non lineare. Il progetto del controllo è stato implementato anche in una simulazione numerica nel dominio del tempo (ossia un’integrazione diretta) per comprovare le prestazioni di riduzione delle vibrazioni da parte del controllo dell’attuatore. Per la modalità di eccitazione è stato utilizzato lo stesso approccio di controllo, in combinazione con un offset di spostamento che rappresenta l’eccitazione della torre fino al valore di spostamento desiderato. Questo offset è una funzione sinusoidale basata sulla frequenza fondamentale rilevata in ciascuna direzione. L’uscita del controllo per controbilanciare la variazione dello spostamento della sommità dovuto ad altri disturbi viene poi modulata sulla funzione sinusoidale di offset e il valore di controllo viene adattato di conseguenza.

Il controllo lineare del feedback, che attenua la risposta dinamica della torre in direzione perpendicolare all’eccitazione, consente al comando di forza inviato all’attuatore di essere pari alla specifica somma lineare pesata delle sette misurazioni dinamiche del programma. Le sette misurazioni sono: le accelerazioni del TMD e della torre, le velocità del TMD e della torre, gli spostamenti del TMD e della torre e lo spostamento relativo del TMD rispetto alla torre. È importante notare che i fattori di pesatura sono valori scalari semplici, positivi o negativi. La parametrizzazione dei fattori di pesatura è basata sui test dinamici sperimentali della torre. Il feedback dell’attuatore attivo viene calcolato istantaneamente (50 Hz)
e i fattori di pesatura sono valori scalari che non utilizzano alcun tipo di funzione di trasferimento dipendente dalla frequenza. Inoltre, il feedback è una combinazione lineare della proprietà dinamica. Non viene utilizzata alcuna manipolazione o logica non lineare. Il progetto del controllo è stato implementato nell’ambito di una simulazione numerica nel dominio del tempo (integrazione diretta) per cui, per ogni intervallo di tempo, è stato possibile adattare l’input della forza verso la massa del TMD tramite il controllo dell’attuatore. La Figura 12 illustra i risultati della simulazione relativa alla soppressione delle vibrazioni – gli scostamenti della torre e il relativo spostamento della massa del TMD.


Per la modalità di eccitazione, è stato utilizzato lo stesso approccio di controllo, in combinazione con un offset che rappresenta l’eccitazione della torre fino al valore di spostamento desiderato. Questo offset è una funzione sinusoidale basata sulla frequenza fondamentale rilevata in ciascuna direzione. L’uscita del controllo per controbilanciare la variazione dello spostamento della sommità dovuto al disturbo viene poi modulata sulla funzione sinusoidale di offset
e il valore di controllo deve essere adattato in modo corrispondente. Per questo offset è stato stabilito in via sperimentale un fattore di pesatura. La Figura 13 mostra i risultati numerici con disturbo dovuto a carico da raffiche di vento per la modalità di eccitazione, con una semplice eccitazione sinusoidale e con l’algoritmo di controllo applicato.


8.0 Progetto di sicurezza
Considerando la forza di +/- 40 kN che può essere fornita dagli azionamenti lineari utilizzati come attuatori, è indispensabile un progetto di sicurezza per assicurare che gli spostamenti della torre non superino i llimiti di fatica. Questo vale anche se l’uscita di forza non è sufficiente a causare deflessioni della sommità maggiori dei +/- 200 mm prestabiliti. Un approccio per migliorare la sicurezza del sistema era quello di aumentare la ridondanza dei sensori di monitoraggio che registrano la deflessione della sommità della torre. Il modo migliore per farlo consiste nell’applicazione di un sistema di monitoraggio aggiuntivo indipendente che, nel caso ideale, utilizza un principio di misurazione diverso da quello dell’hardware di controllo vero e proprio. Per il progetto qui presentato, l’hardware di controllo prevedeva, come sopra indicato, accelerometri e una soglia definita di accelerazione per il filtraggio passa-banda del segnale nell’intervallo di frequenze naturali rilevanti per la struttura. Il sistema di monitoraggio sovraordinato prioritario è un Sistema satellitare globale di navigazione (GNSS) con un’accuratezza di +/- 10 mm. Il sistema GNSS richiede una stazione di base di riferimento che elabora i dati relativi alle coordinate per ricavare i valori di risposta dello scostamento vero e proprio. Se la sommità della torre supera una soglia predeterminata durante il modo di eccitazione artificiale, un fatto che può essere dovuto al vento o ad altra eccitazione, un relè commuta il segnale di attesa su 0 V e ciò provoca l’interruzione del modo di eccitazione. In più, entrambi i sistemi di monitoraggio controllano costantemente i dati acquisiti, individuando segnali da sensori difettosi che provocano anch’essi l’interruzione del modo di eccitazione attivo. I segnali difettosi di accelerazione/di estensione del cavo vengono rilevati attraverso un criterio spettrale di rilevamento dei picchi – è possibile presumere che i sensori forniscano segnali legittimi solo se il rilevamento dei picchi è possibile in un intervallo pertinente. Mentre il sistema GNSS analizza la modifica dei dati relativi alle coordinate, se i dati campionati non cambiano in tempo si presume automaticamente che il segnale sia difettoso.
9.0 Prove delle vibrazioni
I test iniziali delle vibrazioni della torre sono stati effettuati allo stato attuale, con la torre non ancora completata, per cui le frequenze fondamentali della torre a questo stadio risultano al di sopra dell’intervallo di taratura specificato del sistema TMD passivo. Il TMD viene regolato sulla frequenza di taratura massima possibile. L’obiettivo delle prove delle vibrazioni consisteva da una parte nel determinare le frequenze fondamentali della torre con il sistema TMD bloccato e dall’altra determinare lo smorzamento strutturale. Era inoltre necessario determinare il comportamento dinamico con il TMD passivo in funzione, oltre all’aumento dello smorzamento strutturale dovuto al TMD stesso. Per identificare le frequenze naturali fondamentali della torre è possibile utilizzare il metodo della densità spettrale di potenza [1] normalizzata media (ANPSD). A questo scopo, i diagrammi nel dominio del tempo registrati devono essere divisi in segmenti, i quali devono essere trasformati nel dominio della frequenza. Gli spettri risultanti devono essere normalizzati e ne deve essere calcolata la media; quindi devono essere moltiplicati per gli spettri coniugati complessi.
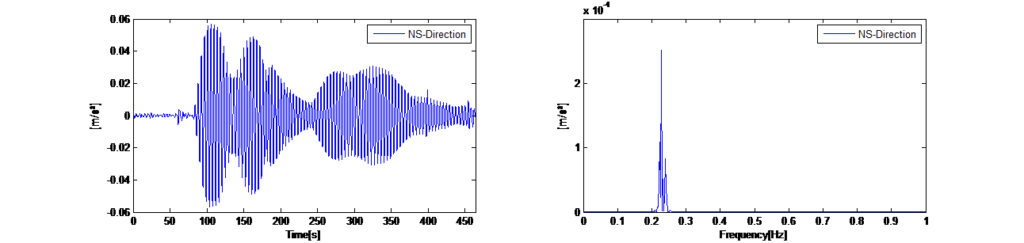
Così facendo vengono eliminate tutte le vibrazioni casuali e solo le vibrazioni libere ricorrenti della struttura verranno visualizzate nello spettro medio, che ora rappresenta le frequenze naturali della torre con l’eccitazione dominante. La Figura 14 a sinistra mostra gli storici temporali registrati delle vibrazioni ambientali orizzontali nelle direzioni x e y con il TMD bloccato. La Figura 14 a destra mostra gli spettri Auto Power medi di una finestra di 120 secondi. Gli spettri indicano che la torre evidenzia una risposta dinamica a due frequenze dominanti (0,225 Hz in direzione x e 0,245 Hz in direzione y).
Oltre al sopra citato metodo spettrale della potenza media – nel quale si presume che la sollecitazione ambientale provochi una risposta dinamica, nei modi di vibrare rilevanti, sufficiente ad ottenere una sicurezza stocastica – le frequenze naturali sono state determinate utilizzando il software di elaborazione dei segnali ARTEMIS, [1] che include i metodi di decomposizione ampliata del dominio della frequenza e di identificazione del sottospazio stocastico.

La decomposizione amplificata del dominio della frequenza (Enhanced Frequency Domain Decomposition, EFDD) e l’identificazione del sottospazio stocastico sono tecniche ampiamente utilizzate per l’identificazione dei parametri modali output-only.


Poiché il metodo EFDD si basa sul calcolo degli spettri di risposta, sono necessarie lunghe registrazioni per mantenere basso l’errore relativo alla stima dello spettro ed estrarre i parametri modali in modo affidabile. L’algoritmo di identificazione del sottospazio stocastico è stato utilizzato per identificare ponti utilizzando un modello output-only. I metodi di identificazione del sottospazio stocastico funzionano nel dominio del tempo e si basano una descrizione spaziale dello stato del problema dinamico. I risultati dell’identificazione del sistema con diversi ordini del modello vengono confrontati per distinguere tre modi strutturali dai modi spuri nei cosiddetti diagrammi di stabilizzazione, i quali rappresentano un’opzione diffusa per selezionare il modello del sistema identificato, in quanto i veri modi strutturali tendono a essere stabili nei successivi ordini dei modelli, soddisfacendo certi criteri di stabilizzazione che vengono valutati in una procedura automatizzata. La Figura 15 illustra uno schema di stabilità risultante dai dati dell’ambiente registrati, dai quali possono essere determinati i modi rilevanti. I modi identificati e i rapporti di smorzamento individuati per ciascun modo nello stato con TMD bloccato (a sinistra) e TMD in funzione (a destra) vengono illustrati anch’essi nella Figura 14. È possibile notare un aumento dello smorzamento strutturale. Lo smorzamento strutturale aggiuntivo rientra nell’intervallo di un valore teorico che può essere determinato a partire dal modello teorico per il quale è stata considerata la configurazione del TMD non tarato.
Oltre alle prove delle vibrazioni ambientali con il sistema TMD passivo, sono state effettuate prove preliminari con il sistema di eccitazione attiva, nonostante il TMD non fosse stato ancora tarato. La Figura 12 a sinistra illustra il diagramma delle accelerazioni nel dominio del tempo registrate sulla sommità della torre. Dopo un’eccitazione sinusoidale iniziale, l’algoritmo del livello di accelerazione costante è stato attivato per determinare in via sperimentale la correlazione tra la deflessione della torre e lo spostamento forzato della massa del TMD. il diagramma nel dominio del tempo illustrato nella Figura 12 visualizza i due scenari di test nel modo di eccitazione e gli spettri FFT corrispondenti mostrano l’evidente risposta della torre nelle sue due frequenze fondamentali (nelle direzioni x e y). La sezione temporale evidenziata in verde è un’eccitazione sinusoidale della massa con controllo attivo disabilitato, che ha causato una risposta dinamica in entrambe le direzioni principali. Lo spettro FFT risultante visualizza i due picchi per identificare le frequenze fondamentali in queste due direzioni. La finestra temporale evidenziata in blu riguarda un’eccitazione con controllo attivo in funzione che ha causato uno spostamento della torre più costante, prevalentemente in una direzione. Il risultante decadimento delle vibrazioni dopo la disattivazione del modo di eccitazione è stato utilizzato anche per determinare lo smorzamento strutturale ed è risultato pari a D=2,4%. Questo risultato coincide con il rapporto di smorzamento determinato con gli algoritmi SSI.

10.0 Conclusione e previsioni
Sulla Thyssen Krupp Test Tower, di 246 m di altezza, è stato installato un TMD a doppio effetto con l’obiettivo di eccitare intenzionalmente la torre fino a una riposta dinamica controllata nelle sue frequenze fondamentali. L’obiettivo di questa eccitazione è ottenere un’oscillazione controllata nelle due direzioni principali della torre. Sulla base di calcoli numerici, è stato ricavato che era necessaria una massa del TMD di 240 t per ottenere lo smorzamento supplementare richiesto per la modalità passiva e per generare la forza di controllo necessaria a ottenere uno spostamento della sommità della torre di +/- 200 mm. Per creare un livello di spostamento costante nella modalità di eccitazione e sopprimere gli spostamenti provocati dal vento, nonché la componente di vibrazione forzata nella direzione perpendicolare, è stato sviluppato un algoritmo di controllo, testato con simulazioni numeriche. Dopo l’installazione del TMD a pendolo passivo, per il quale sono state utilizzate delle lastre prefabbricate di cemento come massa di reazione, sono stati messi in servizio gli attuatori e sono stati effettuati i test iniziali, i quali hanno rivelato che lo smorzamento intrinseco della torre era maggiore di quanto previsto, ma è stato possibile determinare chiaramente tutti i modi significativi. Il modo di eccitazione attivo dell’edificio funziona ed è stato possibile testarlo, anche se non completamente, per derivare tutti parametri operativi, dal momento che l’edificio non è ancora del tutto ultimato. Dato che l’edificio non era stato ancora completato, non è stato possibile adeguare il TMD passivo alle frequenze fondamentali stabilite.
Una volta adattato il sistema TMD, saranno effettuate ulteriori prove nell’edificio, che comprenderanno anche test riguardanti lo smorzamento in dipendenza dall’ampiezza di oscillazione e l’intero progetto di sicurezza.
RIFERIMENTI
[1] Wenzel, H., Pichler, D., Schedler, R. (1991). „Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken“, Bauingenieur 74
[2] Döhler, M., Andersen, P.: Mevel, L. (2012). “Operational Modal Analysis using a Fast Stochastic Subspace Identification Method”, Conference Proceedings of the Society for Experimental Mechanics Series
[3] Soong, T.T., Spencer, J.R. (2000). “Active, Semi-Active and hybrid control of structures” In 12th World Conference for Earthquake Engineering
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003). Passive and active mass damper control of the response of tall buildings to wind gustiness. Eng. Struct., 25, 1199–1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings. J. Eng. Mech. 2004, 130, 437–446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building. Earthq. Eng. Struct. Dyn. 2001, 30, 1655–1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower. CTBUH J. 2012, 24–29.
[8] Soong, T.T. “Active Structural Control: Theory and Practice”; John Wiley & Sons, Inc.: New York, NY, USA, 1990
[9] Preumont, A., Kazuto, S. (2008).”Active Control of Structures”, Wiley, Padstow
1.0 Introduzione/ storia
Nella Germania sud-occidentale è stata costruita una torre di 246 m di altezza per ospitare una struttura di prova per soluzioni innovative per gli ascensori. La torre ha un’impronta al suolo circolare con un diametro di 20 m e offre uno spazio di 9 vani per la prova degli ascensori, un ascensore antincendio e un ascensore a vista panoramica in vetro. È inoltre presente uno scambio di 220 m da utilizzare come vano per il sollevamento meccanico, destinato alla realizzazione dei programmi di prova.
La base della torre ha un diametro di 40 m per fornire ulteriore spazio alle strutture di servizio, alla zona di ingresso e a un centro di formazione. Al livello di 232 m, una piattaforma di osservazione – la più alta della Germania – consente una visione spettacolare della Foresta Nera e, durante le giornate limpide, persino delle Alpi.

2.0 Sistema strutturale
Il sistema strutturale della Test Tower è costituito, fondamentalmente, da un cilindro di cemento armato con un diametro di 20,8 m, ancorato per 30 m all’interno del terreno circostante (si veda la Figura 2). Fino a 110 m di altezza, il cilindro ha uno spessore di 40 cm, dopodiché di 25 cm. Il terreno, costituito da uno strato di Keuper e da calcare fossilifero sottostante, fornisce un’elevata capacità portante, perciò non si è resa necessaria una fondazione su pali. Oltre all’ancoraggio nel terreno circostante, la struttura allargata della base della torre fornisce ulteriore rigidezza laterale.
L’irrigidimento interno del cilindro in cemento armato è realizzato principalmente grazie alle pareti interne dei vani ascensore. Solo a determinati livelli di altezza sono state installate lastre prefabbricate per soffitti per consentire l’accesso ai vani ascensore. Alcuni vani ascensore terminano a un’altezza di 115 m e sono coperti da pavimentazioni a campata lunga con uno spessore di 40 cm, gettate in opera. Questi pavimenti vengono utilizzati per la zona uffici. Al di sopra, uno spazio vuoto fino a un livello di 197 m viene utilizzato come riserva di calore e per il sistema TMD. La parte alta della torre viene utilizzata come zona uffici e per i restanti vani ascensore.

Una caratteristica distintiva della Test Tower è la facciata tessile, realizzata con una maglia in fibra di vetro rivestita con PTFE. La larghezza dell’apertura della maglia aumenta con l’altezza dell’edificio per andare a incrementare la semitrasparenza della facciata, diminuire la densità e il peso del materiale e per gli effetti aerodinamici.
La forma a spirale della facciata è progettata per funzionare come un’elica Scruton e il tessuto stesso contribuisce a ombreggiare la struttura in cemento per evitare le sollecitazioni termiche dovute alla radiazione solare. Nell’ambito della progettazione della facciata e della scelta dei materiali è stato necessario considerare gli aspetti relativi all’installazione, alla manutenzione e alla durata, oltre al carico aerodinamico.
3.0 Metodo di costruzione

La costruzione della Test Tower è stata effettuata nelle seguenti fasi:
- Scavo di una fossa di costruzione circolare di 30 m per la base della torre. Lo scavo e la forma sono stati ottenuti tramite un’esplosione iniziale. Dopo lo scavo, la fossa è stata messa in sicurezza con tiranti nel terreno e rivestimento in calcestruzzo.
- Getto della fondazione a zattera
- Costruzione della struttura verticale in cemento utilizzando casseforme rampanti. Tutte le pareti sono state costruite in maniera continua in un periodo di 4 mesi.
- Costruzione delle solette per i pavimenti.
- Costruzione della zona di ingresso.
4.0 Risposta dinamica prevista al carico aerodinamico
Le frequenze fondamentali per la Test Tower sono state previste nell’intervallo 0,17 – 0,20 Hz, in base alla fase di costruzione e allo stato del cemento (con o senza crepe) – si veda la Figura 4.

L’analisi aerodinamica ha rivelato che la sollecitazione risonante con la struttura può verificarsi in presenza di velocità del vento corrispondenti a valori al suolo (altezza 10 m) compresi nell’intervallo 55 – 60 km/h. Era previsto che, in assenza di ulteriore smorzamento, questa sollecitazione risonante potesse causare spostamenti sulla sommità di circa +/- 750 mm che, oltre a pregiudicare il comfort degli occupanti, avrebbero anche avuto conseguenze significative sulla ressistenza a fatica in esercizio della struttura in cemento della torre (si veda la Figura 5). Per ridurre la risposta dinamica alla sollecitazione da vento trasversale, è stato realizzato un sistema di smorzamento passivo a massa accordata. Poiché la torre sarebbe stata utilizzata come ambiente di prova per attrezzature relative agli ascensori, sensibili alle oscillazioni, il proprietario era alla ricerca di una possibilità di sollecitazione artificiale della torre durante le giornate di calma, tuttavia con scostamenti che non provocassero problemi di affaticamento. Il livello richiesto per il movimento oscillatorio artificiale rientrava nell’intervallo, considerato sicuro, di circa +/- 200 mm. Questa richiesta ha fornito la rara opportunità di realizzare uno smorzatore a massa ibrido (HMD) oppure, visto che il sistema di progettazione differisce da quello degli altri sistemi HMD introdotti in passato, un cosiddetto TMD a duplice uso. Il sistema verrà presentato nei capitoli seguenti, assieme all’ottimizzazione del sistema passivo, alla progettazione del meccanismo degli attuatori, agli algoritmi di controllo e al progetto di sicurezza.

5.0 Ottimizzazione del sistema di smorzamento a massa accordata passivo
Per la determinazione dei parametri del sistema TMD passivo è stato necessario considerare tre diversi aspetti: a) fornire uno smorzamento strutturale aggiuntivo sufficiente a ridurre la risposta dinamica dovuta alla sollecitazione per dissipazione dei vortici, b) limitare il conseguente scostamento della massa principale del TMD in modalità passiva a un valore realizzabile/pratico nei momenti di sollecitazione da raffiche di venti trasversali e c) scegliere la massa del TMD in base alla quantità di energia necessaria per ottenere la deflessione massima della torre nella modalità di sollecitazione, considerando i limiti prestazionali consentiti dagli attuatori forniti (ossia la massima forza generata e la corsa massima durante il funzionamento). Per ottimizzare il sistema TMD, è stato utilizzato un modello numerico in cui erano rappresentati la distribuzione della massa della torre e i momenti di inerzia della massa documentati nelle proprietà strutturali identificate. Anche gli elementi di irrigidimento tra i piani sono stati adattati in modo da corrispondere alle forme modali e alle frequenze naturali durante le osservazioni a piena scala. La Figura 6 a sinistra mostra le forme modali e le frequenze naturali di questo modello analogico utilizzato. La Figura 6 a sinistra confronta anche le curve modali del modello analogico con quelle del modello dettagliato preparato dal consulente strutturale.


Inoltre, il TMD è stato modellato in modo discreto, come un sistema a pendolo, tenendo conto anche della sua posizione eccentrica sulla torre. Le caratteristiche di carico nel caso di input in esame, ossia la sollecitazione risonante dovuta al distacco di vortice, sono molto simili a quelle di una singola eccitazione armonica. Tuttavia, il carico contemporaneo dovuto alle raffiche di vento è, intrinsecamente, di natura stocastica e ad esso si applicano criteri di ottimizzazione diversi dal conosciuto criterio di Den Hartog. In più, gli spostamenti relativi della massa del TMD sono maggiori quando il carico è di tipo stocastico piuttosto che armonico. Poiché, per la determinazione numerica dei parametri ottimali per il TMD, è necessario considerare un carico simile a quello reale, è stato generato uno storico temporale comprendente sia il carico stocastico dovuto alle raffiche (basato sullo spettro di Davenport) e un componente con una risonanza sovrapposta, simile a quella della dissipazione dei vortici, per rappresentare la sollecitazione totale da vento trasversale (si veda la Figura 3 a destra). La riduzione della deflessione della torre che può essere ottenuta con il sistema TMD passivo ottimizzato, nonché gli scostamenti del TMD risultanti, sono illustrati nella Figura 3 a destra. In base a questi risultati relativi a uno smorzamento strutturale intrinseco stimato in ξ=0,8%, è stato calcolato che era necessaria una massa del TMD di 240 t per mantenere gli scostamenti entro +/- 650 mm, preservando al contempo un coefficiente di smorzamento ottimale per il TMD, in modo da ottimizzare le prestazioni di quest’ultimo. Un aumento dello smorzamento del TMD avrebbe ridotto la corsa, mentre l’efficacia sarebbe rimasta comunque sufficiente; ciò tuttavia avrebbe avuto implicazioni negative sui requisiti relativi alle forze sugli attuatori. Per la determinazione delle forze necessarie per la configurazione ottimale del TMD da 240 t è stato utilizzato anche il modello analogico per verificare che, con una forza massima di 40 kN dagli attuatori, fosse possibile ottenere deflessioni della torre entro l’intervallo di +/- 200 mm. La Figura 4 illustra i risultati di una simulazione numerica nel dominio del tempo in base al modello numerico analogico; in questo caso vengono visualizzate le oscillazioni massime risultanti della sommità della torre, le oscillazioni della massa del TMD e le forze in ingresso attive che le provocano.


6.0 Descrizione del sistema di controllo
La dualità del sistema di controllo serve allo scopo a) di ridurre i consumi di energia, durante il normale funzionamento passivo, riducendo le vibrazioni che si verificano e b) di ridurre i requisiti relativi alle forze sugli attuatori, utilizzando effetti di risonanza per eccitare la massa principale del TMD soddisfacendo così, alla fine, la domanda di forza effettiva. Pertanto, rispetto ad altri sistemi di controllo (si veda la Figura 1), gli attuatori collegano la struttura principale alla massa del TMD, ma non vengono utilizzati per controllare direttamente tale massa, come normalmente accade in un tipico sistema con azionamento massa/smorzatore attivo. Per il duplice uso implementato, è stata scelta una massa di reazione per l’azionamento passivo di 240 tonnellate. Per la modalità di eccitazione, due attuatori lineari – uno in ciascuna direzione principale – vengono collegati alla massa del TMD vicino al centro di gravità della massa, per evitare qualsiasi artefatto torsionale. Ogni attuatore lineare può fornire forze fino a 40 kN entro una corsa di max +/- 600 mm (si veda il dettaglio nella Figura 2). Gli azionamenti lineari possono essere staccati, in modo tale che la modalità completamente passiva non venga influenzata dai cuscinetti degli attuatori, nel raro caso di un loro guasto.


Il sistema è dotato di quattro accelerometri monoassiali (K-beam sismico/MEMS; uno in ogni direzione) per determinare il livello della sommità della torre e le accelerazioni della massa del TMD. I segnali di accelerazione vengono filtrati in un filtro passa-banda entro l’intervallo di frequenze naturali fondamentali della torre (0,1 – 0,3 Hz) e integrati per ottenere le velocità e le deflessioni della torre. In più, i valori di scostamento integrati possono essere confrontati con quelli di un sistema di navigazione satellitare globale aggiuntivo, installato anch’esso sulla sommità per individuare derive dei segnali. A questo proposito è stato effettuato un test di correlazione iniziale. Inoltre, gli spostamenti del TMD vengono monitorati direttamente con estensimetri e un sistema induttivo di misurazione della lunghezza integrato nei motori lineari.
7.0 Algoritmo di controllo
Il ciclo di controllo generale della torre è illustrato alla Figura 5, che descrive la sequenza di controllo a ciclo chiuso. Una progettazione dettagliata dell’algoritmo di controllo richiederebbe modelli analitici dell’interazione tra attuatori e massa del TMD per determinare la connessione tra l’input dell’attuatore e la forza applicata all’azione. Questi modelli dovrebbero essere combinati con il modello analitico della struttura principale, che descrive il comportamento dinamico generale dell’edificio. Inoltre, rispetto agli algoritmi di controllo standard utilizzati per altre applicazioni HMD come in [2],[3] o ricercati in via teorica come in [1] l’algoritmo di controllo da applicare a questa torre doveva tenere conto di un’eccitazione sincrona controllata in una direzione principale e la riduzione delle vibrazioni in direzione perpendicolare. Dato che la risposta dinamica è prevista prevalentemente nei modi fondamentali, è stato possibile utilizzare, per entrambe queste operazioni, il controllo lineare del feedback, con tutti i suoi vantaggi di prevenzione delle instabilità. Questo perché la semplice realizzazione implementata per il controllo, il controllo lineare del feedback, che attenua la risposta dinamica della torre in direzione perpendicolare all’eccitazione, agisce sull’attuatore corrispondente attraverso una specifica somma lineare pesata di sette misurazioni dinamiche strutturali. Queste misurazioni sono: le accelerazioni del TMD e della sommità della torre, le velocità del TMD e della sommità della torre, gli scostamenti del TMD e della sommità della torre e lo scostamento relativo del TMD rispetto alla sommità della torre. È importante notare che i fattori di pesatura preselezionati sono guadagni scalari semplici, positivi o negativi. La parametrizzazione dei fattori di pesatura è basata sui test dinamici della torre e non utilizza alcuna modifica dipendente dalla frequenza. Il feedback dell’attuatore attivo viene calcolato istantaneamente (a 50 Hz) ed è, nuovamente, una combinazione lineare delle misurazioni dinamiche precedenti. Non viene utilizzata alcuna manipolazione non lineare. Il progetto del controllo è stato implementato anche in una simulazione numerica nel dominio del tempo (ossia un’integrazione diretta) per comprovare le prestazioni di riduzione delle vibrazioni da parte del controllo dell’attuatore. Per la modalità di eccitazione è stato utilizzato lo stesso approccio di controllo, in combinazione con un offset di spostamento che rappresenta l’eccitazione della torre fino al valore di spostamento desiderato. Questo offset è una funzione sinusoidale basata sulla frequenza fondamentale rilevata in ciascuna direzione. L’uscita del controllo per controbilanciare la variazione dello spostamento della sommità dovuto ad altri disturbi viene poi modulata sulla funzione sinusoidale di offset e il valore di controllo viene adattato di conseguenza.

Il controllo lineare del feedback, che attenua la risposta dinamica della torre in direzione perpendicolare all’eccitazione, consente al comando di forza inviato all’attuatore di essere pari alla specifica somma lineare pesata delle sette misurazioni dinamiche del programma. Le sette misurazioni sono: le accelerazioni del TMD e della torre, le velocità del TMD e della torre, gli spostamenti del TMD e della torre e lo spostamento relativo del TMD rispetto alla torre. È importante notare che i fattori di pesatura sono valori scalari semplici, positivi o negativi. La parametrizzazione dei fattori di pesatura è basata sui test dinamici sperimentali della torre. Il feedback dell’attuatore attivo viene calcolato istantaneamente (50 Hz) e i fattori di pesatura sono valori scalari che non utilizzano alcun tipo di funzione di trasferimento dipendente dalla frequenza. Inoltre, il feedback è una combinazione lineare della proprietà dinamica. Non viene utilizzata alcuna manipolazione o logica non lineare. Il progetto del controllo è stato implementato nell’ambito di una simulazione numerica nel dominio del tempo (integrazione diretta) per cui, per ogni intervallo di tempo, è stato possibile adattare l’input della forza verso la massa del TMD tramite il controllo dell’attuatore. La Figura 12 illustra i risultati della simulazione relativa alla soppressione delle vibrazioni – gli scostamenti della torre e il relativo spostamento della massa del TMD.


Per la modalità di eccitazione, è stato utilizzato lo stesso approccio di controllo, in combinazione con un offset che rappresenta l’eccitazione della torre fino al valore di spostamento desiderato. Questo offset è una funzione sinusoidale basata sulla frequenza fondamentale rilevata in ciascuna direzione. L’uscita del controllo per controbilanciare la variazione dello scostamento della sommità dovuto ad altri disturbi viene poi modulata sulla funzione sinusoidale di offset e il valore di controllo deve essere adattato di conseguenza. Per questo offset è stato stabilito in via sperimentale un fattore di pesatura. La Figura 13 mostra i risultati numerici con disturbo dovuto a carico da raffiche di vento per la modalità di eccitazione, con una semplice eccitazione sinusoidale e con l’algoritmo di controllo applicato.


8.0 Progetto di sicurezza
Considerando la forza di +/- 40 kN che può essere fornita dagli azionamenti lineari utilizzati come attuatori, è indispensabile un progetto di sicurezza per assicurare che gli spostamenti della torre non superino i llimiti di fatica. Questo vale anche se l’uscita di forza non è sufficiente a causare deflessioni della sommità maggiori dei +/- 200 mm prestabiliti. Un approccio per migliorare la sicurezza del sistema era quello di aumentare la ridondanza dei sensori di monitoraggio che registrano la deflessione della sommità della torre. Il modo migliore per farlo consiste nell’applicazione di un sistema di monitoraggio aggiuntivo indipendente che, nel caso ideale, utilizza un principio di misurazione diverso da quello dell’hardware di controllo vero e proprio. Per il progetto qui presentato, l’hardware di controllo prevedeva, come sopra indicato, accelerometri e una soglia definita di accelerazione per il filtraggio passa-banda del segnale nell’intervallo di frequenze naturali rilevanti per la struttura. Il sistema di monitoraggio sovraordinato prioritario è un Sistema satellitare globale di navigazione (GNSS) con un’accuratezza di +/- 10 mm. Il sistema GNSS richiede una stazione di base di riferimento che elabora i dati relativi alle coordinate per ricavare i valori di risposta dello scostamento vero e proprio. Se la sommità della torre supera una soglia predeterminata durante il modo di eccitazione artificiale, un fatto che può essere dovuto al vento o ad altra eccitazione, un relè commuta il segnale di attesa su 0 V e ciò provoca l’interruzione del modo di eccitazione. In più, entrambi i sistemi di monitoraggio controllano costantemente i dati acquisiti, individuando segnali da sensori difettosi che provocano anch’essi l’interruzione del modo di eccitazione attivo. I segnali difettosi di accelerazione/di estensione del cavo vengono rilevati attraverso un criterio spettrale di rilevamento dei picchi – è possibile presumere che i sensori forniscano segnali legittimi solo se il rilevamento dei picchi è possibile in un intervallo pertinente. Mentre il sistema GNSS analizza la modifica dei dati relativi alle coordinate, se i dati campionati non cambiano in tempo si presume automaticamente che il segnale sia difettoso.
9.0 Prove delle vibrazioni
I test iniziali delle vibrazioni della torre sono stati effettuati allo stato attuale, con la torre non ancora completata, per cui le frequenze fondamentali della torre a questo stadio risultano al di sopra dell’intervallo di taratura specificato del sistema TMD passivo. Il TMD viene regolato sulla frequenza di taratura massima possibile. L’obiettivo delle prove delle vibrazioni consisteva da una parte nel determinare le frequenze fondamentali della torre con il sistema TMD bloccato e dall’altra determinare lo smorzamento strutturale. Era inoltre necessario determinare il comportamento dinamico con il TMD passivo in funzione, oltre all’aumento dello smorzamento strutturale dovuto al TMD stesso. Per identificare le frequenze naturali fondamentali della torre è possibile utilizzare il metodo della densità spettrale di potenza [1] normalizzata media (ANPSD). A questo scopo, i diagrammi nel dominio del tempo registrati devono essere divisi in segmenti, i quali devono essere trasformati nel dominio della frequenza. Gli spettri risultanti devono essere normalizzati e ne deve essere calcolata la media; quindi devono essere moltiplicati per gli spettri coniugati complessi.
Così facendo vengono eliminate tutte le vibrazioni casuali e solo le vibrazioni libere ricorrenti della struttura verranno visualizzate nello spettro medio, che ora rappresenta le frequenze naturali della torre con l’eccitazione dominante. La Figura 14 a sinistra mostra gli storici temporali registrati delle vibrazioni ambientali orizzontali nelle direzioni x e y con il TMD bloccato. La Figura 14 a destra mostra gli spettri Auto Power medi di una finestra di 120 secondi. Gli spettri indicano che la torre evidenzia una risposta dinamica a due frequenze dominanti (0,225 Hz in direzione x e 0,245 Hz in direzione y).
Oltre al sopra citato metodo spettrale della potenza media – nel quale si presume che la sollecitazione ambientale provochi una risposta dinamica, nei modi di vibrare rilevanti, sufficiente ad ottenere una sicurezza stocastica – le frequenze naturali sono state determinate utilizzando il software di elaborazione dei segnali ARTEMIS, [1] che include i metodi di decomposizione ampliata del dominio della frequenza e di identificazione del sottospazio stocastico.

La decomposizione amplificata del dominio della frequenza (Enhanced Frequency Domain Decomposition, EFDD) e l’identificazione del sottospazio stocastico sono tecniche ampiamente utilizzate per l’identificazione dei parametri modali output-only.


Poiché il metodo EFDD si basa sul calcolo degli spettri di risposta, sono necessarie lunghe registrazioni per mantenere basso l’errore relativo alla stima dello spettro ed estrarre i parametri modali in modo affidabile. L’algoritmo di identificazione del sottospazio stocastico è stato utilizzato per identificare ponti utilizzando un modello output-only. I metodi di identificazione del sottospazio stocastico funzionano nel dominio del tempo e si basano una descrizione spaziale dello stato del problema dinamico. I risultati dell’identificazione del sistema con diversi ordini del modello vengono confrontati per distinguere tre modi strutturali dai modi spuri nei cosiddetti diagrammi di stabilizzazione, i quali rappresentano un’opzione diffusa per selezionare il modello del sistema identificato, in quanto i veri modi strutturali tendono a essere stabili nei successivi ordini dei modelli, soddisfacendo certi criteri di stabilizzazione che vengono valutati in una procedura automatizzata. La Figura 15 illustra uno schema di stabilità risultante dai dati dell’ambiente registrati, dai quali possono essere determinati i modi rilevanti. I modi identificati e i rapporti di smorzamento individuati per ciascun modo nello stato con TMD bloccato (a sinistra) e TMD in funzione (a destra) vengono illustrati anch’essi nella Figura 14. È possibile notare un aumento dello smorzamento strutturale. Lo smorzamento strutturale aggiuntivo rientra nell’intervallo di un valore teorico che può essere determinato a partire dal modello teorico per il quale è stata considerata la configurazione del TMD non accordato. Oltre alle prove delle vibrazioni ambientali con il sistema TMD passivo, sono state effettuate prove preliminari con il sistema di eccitazione attiva, nonostante lo stato non accordato nel sistema TMD. La Figura 12 a sinistra illustra il diagramma delle accelerazioni nel dominio del tempo registrate sulla sommità della torre. Dopo un’eccitazione sinusoidale iniziale, l’algoritmo del livello di accelerazione costante è stato attivato per determinare in via sperimentale la correlazione tra la deflessione della torre e lo spostamento forzato della massa del TMD. il diagramma nel dominio del tempo illustrato nella Figura 12 visualizza i due scenari di test nel modo di eccitazione e gli spettri FFT corrispondenti mostrano l’evidente risposta della torre nelle sue due frequenze fondamentali (nelle direzioni x e y). La sezione temporale evidenziata in verde è un’eccitazione sinusoidale della massa con controllo attivo disabilitato, che ha causato una risposta dinamica in entrambe le direzioni principali. Lo spettro FFT risultante visualizza i due picchi per identificare le frequenze fondamentali in queste due direzioni. La finestra temporale evidenziata in blu riguarda un’eccitazione con controllo attivo in funzione che ha causato uno spostamento della torre più costante, prevalentemente in una direzione. Il risultante decadimento delle vibrazioni dopo la disattivazione del modo di eccitazione è stato utilizzato anche per determinare lo smorzamento strutturale ed è risultato pari a D=2,4%. Questo risultato coincide con il rapporto di smorzamento determinato con gli algoritmi SSI.

10.0 Conclusione e previsioni
Sulla Thyssen Krupp Test Tower, di 246 m di altezza, è stato installato un TMD a doppio effetto con l’obiettivo di eccitare intenzionalmente la torre fino a una riposta dinamica controllata nelle sue frequenze fondamentali. L’obiettivo di questa eccitazione è ottenere un’oscillazione controllata nelle due direzioni principali della torre. Sulla base di calcoli numerici, è stato ricavato che era necessaria una massa del TMD di 240 t per ottenere lo smorzamento supplementare richiesto per la modalità passiva e per generare la forza di controllo necessaria a ottenere uno spostamento della sommità della torre di +/- 200 mm. Per creare un livello di spostamento costante nella modalità di eccitazione e sopprimere gli spostamenti provocati dal vento, nonché la componente di vibrazione forzata nella direzione perpendicolare, è stato sviluppato un algoritmo di controllo, testato con simulazioni numeriche. Dopo l’installazione del TMD a pendolo passivo, per il quale sono state utilizzate delle lastre prefabbricate di cemento come massa di reazione, sono stati messi in servizio gli attuatori e sono stati effettuati i test iniziali, i quali hanno rivelato che lo smorzamento intrinseco della torre era maggiore di quanto previsto, ma è stato possibile determinare chiaramente tutti i modi significativi. Il modo di eccitazione attivo dell’edificio funziona ed è stato possibile testarlo, anche se non completamente, per derivare tutti parametri operativi, dal momento che l’edificio non è ancora del tutto ultimato. Dato che l’edificio non era stato ancora completato, non è stato possibile adeguare il TMD passivo alle frequenze fondamentali stabilite.
Una volta adattato il sistema TMD, saranno effettuate ulteriori prove nell’edificio, che comprenderanno anche test riguardanti lo smorzamento in dipendenza dall’ampiezza di oscillazione e l’intero progetto di sicurezza.
RIFERIMENTI
[1] Wenzel, H., Pichler, D., Schedler, R. (1991). „Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken“, Bauingenieur 74
[2] Döhler, M., Andersen, P.: Mevel, L. (2012). “Operational Modal Analysis using a Fast Stochastic Subspace Identification Method”, Conference Proceedings of the Society for Experimental Mechanics Series
[3] Soong, T.T., Spencer, J.R. (2000). “Active, Semi-Active and hybrid control of structures” In 12th World Conference for Earthquake Engineering
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003). Passive and active mass damper control of the response of tall buildings to wind gustiness. Eng. Struct., 25, 1199–1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings. J. Eng. Mech. 2004, 130, 437–446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building. Earthq. Eng. Struct. Dyn. 2001, 30, 1655–1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower. CTBUH J. 2012, 24–29.
[8] Soong, T.T. “Active Structural Control: Theory and Practice”; John Wiley & Sons, Inc.: New York, NY, USA, 1990
[9] Preumont, A., Kazuto, S. (2008).”Active Control of Structures”, Wiley, Padstow
Condividi questo articolo
Ulteriori risorse
Vi servono ulteriori informazioni su questo argomento?
Non esitate a contattarci con domande specifiche.
Uno dei nostri ingegneri risponderà entro breve tempo alla richiesta.
Ulteriori risorse
Vi servono ulteriori informazioni su questo argomento?
Non esitate a contattarci con domande specifiche.
Uno dei nostri ingegneri risponderà entro breve tempo alla richiesta.